Les tiges musicales

Dans l'expérience des tiges qui sifflent, on montre que l'on peut créer des ondes longitudinales dans une barre d'aluminium à l'aide de frottements le long de la tige, et produire un son pur.

D'après la relation entre la fréquence f de l'onde, sa longueur d'onde λ et la vitesse de l'onde dans la tige d'aluminium v_Al

f.λ = v_Al

il est possible de faire des notes de fréquence précise en choisissant la longueur des tiges. On peut ainsi fabriquer un instrument de musique.

1 Matériel

• Des tiges d'aluminium de même diamètre, que l'on peut acheter dans n'importe quelle grande surface de bricolage
• Scie a métaux et lime plate
• Oscilloscope ou ordinateur équipé d'un microphone et d'un logiciel d'analyse du son
• Mètre précis
• Calculatrice

2 Préalables sur les gammes musicales

Une gamme musicale est déterminée par les écarts de fréquence entre les notes qui composent la gamme. Il existe un grand nombre de gammes, selon leur origine culturelle.

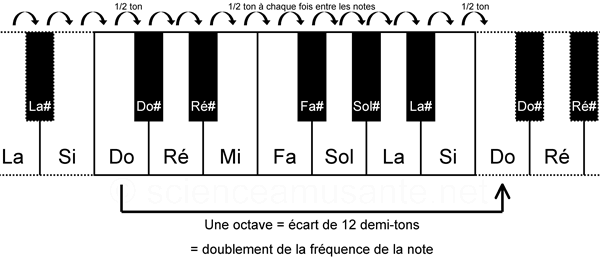
La gamme utilisée dans la musique occidentale classique (et même moderne) est basée sur la gamme tempérée (ou tempérament égal) inventée par Jean-Sébastien Bach. Dans cette gamme il y a 12 notes séparées chacunes d'un demi-ton :

Gamme tempérée de Bach.

La fréquence f_a entre une note donnée et la fréquence f_a' de la même note à l'octave supérieure sont liées par la relation : f_a' = 2 f_a.

Comme cette relation doit être valable pour n'importe quelle note (c'est la contrainte imposée par Bach), on en déduit que le rapport de fréquences de 2 notes successives doit être égal à 2^1/12. Les rapports sont identiques entre n'importe quel couple de notes qui se suivent, d'où le nom de gamme tempérée ou tempérament égal pour cette gamme. Cette gamme n'est cependant pas idéale pour certains styles musicaux ou certains instruments car elle peut conduire à des accords légèrement dissonants pour les mélomanes puristes.

Mais pour des raisons de commodité, c'est cette gamme tempérée que nous utiliserons pour la suite, car l'écart entre les notes est facilement calculable.

L'écart étant fixé entre les notes, il faut alors fixer la fréquence d'une note de référence. C'est actuellement la fréquence du La de la 4^e octave (noté La₄) qui est fixée à 440 Hz. (Voir remarque en dernière section)

3 Protocole

• Les tiges vendues ont souvent une longueur de 1 m. Cependant cette longueur n'est pas toujours très précise. Il convient alors de mesurer précisément cette longueur avec un mètre. Soit L₁ la longueur la longueur de la tige n°1, qui aura la note la plus basse, de fréquence f₁.
• Devant un microphone relié à un oscilloscope ou un ordinateur équipé d'un logiciel d'analyse du son, faire siffler la tige comme décrit dans l'expériences des tiges qui sifflent. Relever la fréquence de la note produite. À titre d'exemple : pour L₁ = 1 m, on obtient f₁ = 2508 Hz.
• Pour calculer la longueur L₂ de la tige qui donnera la note suivante, on utilise la relation

[math]L_1 f_1 = L_2 f_2[/math]

ce qui suppose que la vitesse v_Al des ondes sonores dans la tige d'aluminium est la même quelle que soit la fréquence de la note. Cette approximation est valable pour les fréquences qui nous intéressent. On en déduit alors :

[math]L_2 = L_1\frac{f_1}{f_2}[/math]

Or, par définition de la gamme tempérée de Bach :

[math]f_2 = 2^{\frac{1}{12}} f_1[/math]

D'où :

[math]L_2= L_1 \frac{f_1}{2^{\frac{1}{12}} f_1} = L_1 \frac{1}{2^{\frac{1}{12}}} = 0,94387 L_1[/math]

De même pour les longueurs des tiges pour les notes suivantes :

[math]L_3 = L_2 \frac{1}{2^{\frac{1}{12}}} = 0,94387 L_2[/math]

...

[math]L_{n+1} = L_n \frac{1}{2^{\frac{1}{12}}} = 0,94387 L_n[/math]

Pour L₁ = 1 m, on obtient alors les longueurs suivantes :

Tige i	Li (m)	fi (Hz)
1	1,000	2508
2	0,944	2657
3	0,891	2815
4	0,841	2983
5	0,794	3160
6	0,749	3348
7	0,707	3547
8	0,667	3758
9	0,630	3981
10	0,595	4218
11	0,561	4469
12	0,530	4734
13	0,500	5016
...

Après calcul complet, les longueurs sont arrondies au millimètre et la fréquence au Hz. On retrouve bien que la tige n°13 est de longueur exactement moitié de la tige n°1, car elle joue la note située à l'octave (fréquence double, note située à 12 demi-tons au-dessus). Ceci est d'ailleurs valable pour toutes les notes séparées de 12 demi-tons :

[math]L_{n+12} = L_n \left(\frac{1}{2^{\frac{1}{12}}}\right)^{12} = L_n \frac{1}{\left(2^{\frac{1}{12}}\right)^{12}} = \frac{1}{2} L_n[/math]

• On découpe à l'aide de la scie à métaux les tiges aux longueurs calculées, en prenant soin de bien respecter les longueurs au millimètre près. Les bords de la tige étant tranchant, il est important d'en limer légèrement le tour.
• Nettoyer les tiges avec un essuie-tout imbibé d'eau et sécher.
• Faire siffler les tiges et jouer un morceau sur la gamme obtenue.

4 Gamme absolue et gamme relative

Un peu plus compliqué, pour les musiciens puristes !

• Il est important de préciser que les notes de la gamme obtenue ne correspondent pas forcément aux notes (Do, Do#, Ré, etc.) de la gamme d'un piano par exemple. Nous avons découpé les tiges en prenant comme tige de référence la première, qui a une longueur de 1 m. Or la fréquence de 2508 Hz ne correspondant pas exactement à une note réelle. Par contre, l'écart entre nos notes respecte parfaitement l'écart déterminé par Bach. Notre gamme est donc une gamme relative et non une gamme absolue.
• Pour obtenir une gamme absolue, en faisant en sorte que la première tige corresponde à un Do (par exemple), il faudrait fixer la longueur L₁ telle que f₁ corresponde à un vrai Do. Le plus simple consiste alors à prendre le premier Do dont la fréquence est immédiatement supérieure à 2508 Hz. En se fixant comme convention f_La4 = 440 Hz, les fréquences des La aux autres octaves sont :

Octave i	Lai	fLai (Hz)
1	La1	55
2	La2	110
3	La3	220
4	La4	440 (par convention)
5	La5	880
6	La6	1760
7	La7	3520
8	La8	7040
9	La9	14080

On voit donc que le premier Do possible au delà de 2508 Hz est le Do₈ qui se trouve après le La₇. Ce Do₈ a pour fréquence calculée : f_Do8 = 2960 Hz. La longueur de la tige équivalente est donc : 0,847 m.